简单的说，Neighbor Embedding是一种降维方法，而且是无监督的，利用的是各个单词的临近关系
Manifold Learning(流形学习)
对于降维问题的思考在于，我们的降维在高维空间和低维空间看到的东西是不同的：
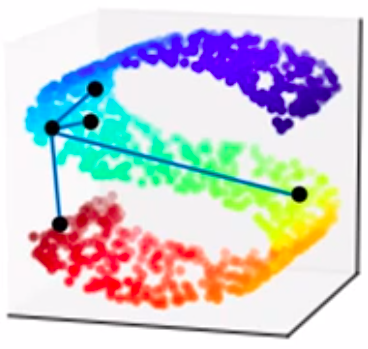
上图很容易看到，蓝色的点距离绿色的点更近、距离红色的点更远。但是如果我们只是简单的压扁，就会造成蓝色的点距离红色的点更近的错觉，这就是降维导致的信息丢失。
我们流形学习的思想就是：拉平这个高维空间，而不是压扁这个高位空间，以防止丢失信息：
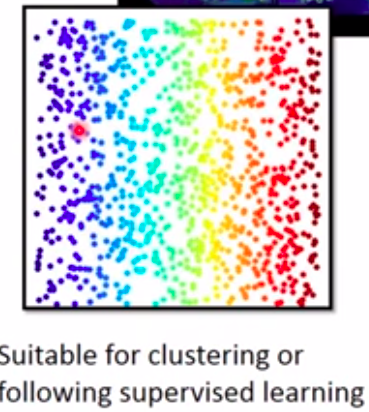
- Locally Linear Embedding(LLE)
这种算法的思路是保持数据中任意一个元素和其临近的K个元素的关系\(w_{i,j}\)保持不变: \(Find\, a\,set\,of\,w_{i,j}\,minimizing\\\sum_{i}\|x^i\,-\,\sum_{j}w_{i,j}x^j\|_2\)
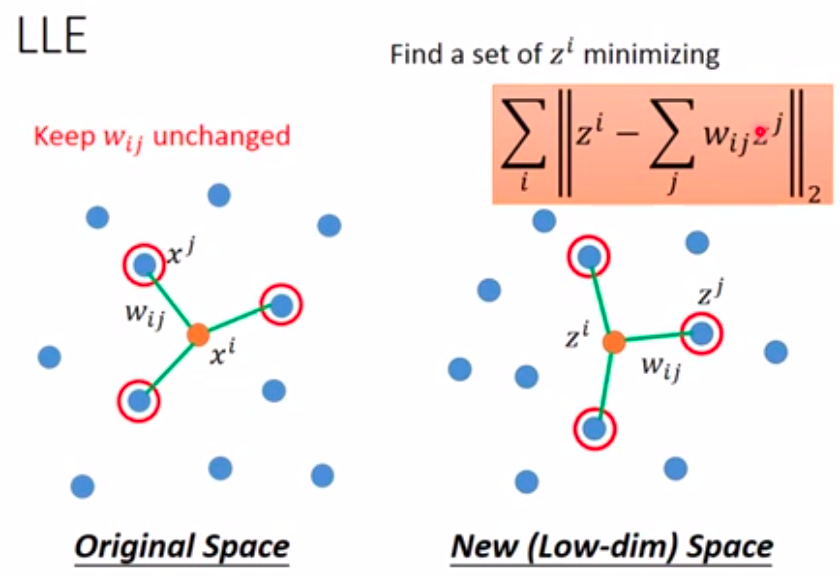
Then find the dimension reduction results \(z^i\) and \(z^j\) based on \(w_{i,j}\):
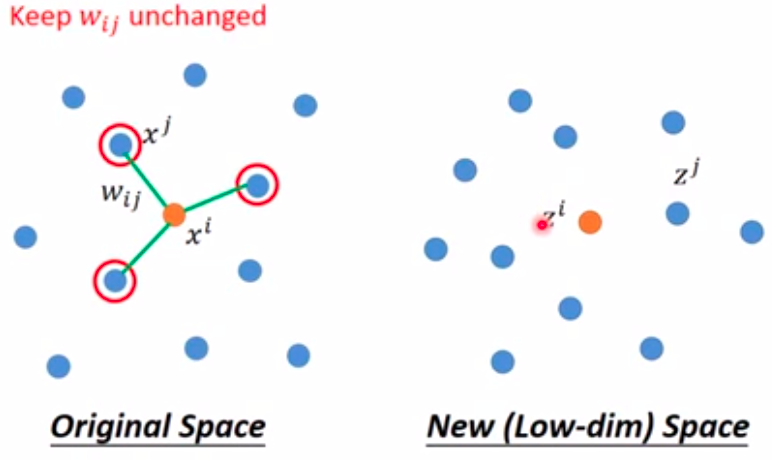降维后的新元素\(z^i\)和\(z^j\)之间，也应该保持上述高维空间的关系，即\(w_{i,j}\)保持不变:
这种关系就和《长恨歌》中的一句诗句类似:
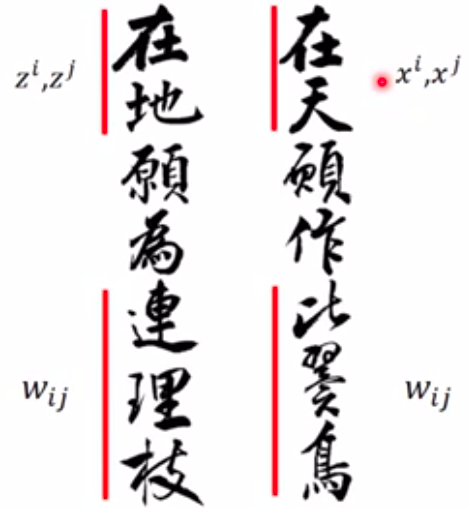
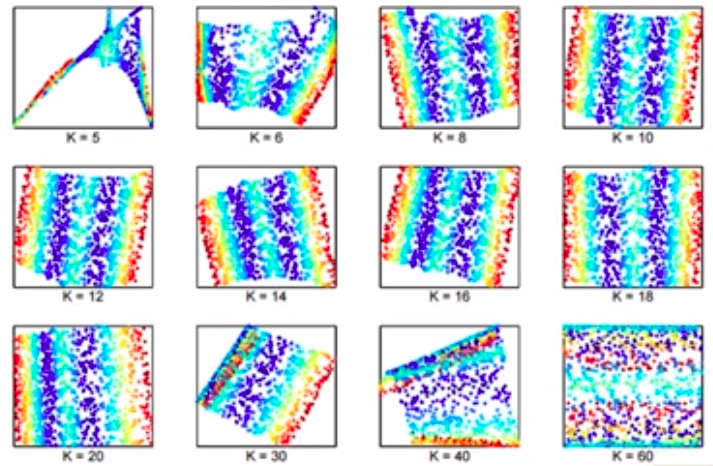
LLE中，K的选择是一个关键要素：K选的少了高维的关系可能无法维系；K选的多了算法的复杂性很大，效果也不好：
- Laplacian Eigenmaps